コンピュータは0と1しか理解できません。では、どうやって様々なデータを表現するのでしょうか。
それを理解する前にコンピュータが数値を扱う仕組みを知っておきましょう。
と本題に入る前にひとつ。ここでの話題は初心者には難しいと思います。
特に後半の話は理解が難しく、それが挫折に繋がるかもしれません。
でも大丈夫! これを知らなくてもエンジニアになれます。良いか悪いか現代のプログラムはこの辺を知らなくても作れます。
実際に僕も専門学校で学んだ時は1ミリも理解できませんでした。難しかったら先に進み、また学習すればいいと思います。
数値の種類
数値にも正数、負数、小数 . . .と色々ありますよね。コンピュータは整数と実数で大きく表現が異なります。
もっと雑に伝えるなら、小数の有無です。この数値をbyte単位で扱うのがコンピュータの基本です。
また、常に忘れないで欲しいのは整数でも実数でもコンピュータは0と1の集合としか理解してません。
ここでの話も人間が理解できるように0と1を解釈してるに過ぎません。
符号の表現
整数には正負の数値が存在しますが、僕たち人間はどうやって区別するのでしょうか。

数字の頭にプラスかマイナスを付けて表現します。

そうだね。つまり1bit利用すれば、その数値が正負のどちらかを表現できるね。
この考え方を採用して符号が付いてる整数を符号付き(signed)整数と言います。
対して符号が付いていない整数は符号なし(unsigned)整数と呼ばれます。
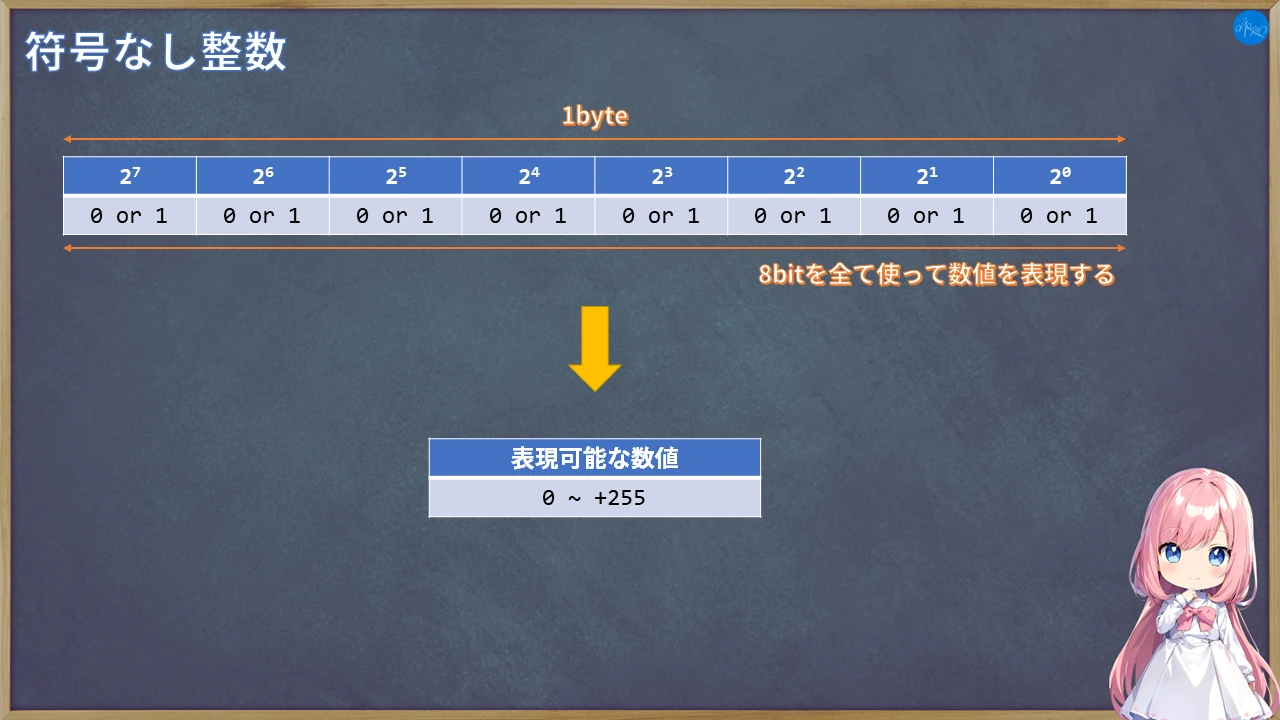
符号なし(unsigned)整数
符号なし整数の場合、全てのbitを数値のために利用できます。つまり単純に2のbit乗だけ数値を表現できます。
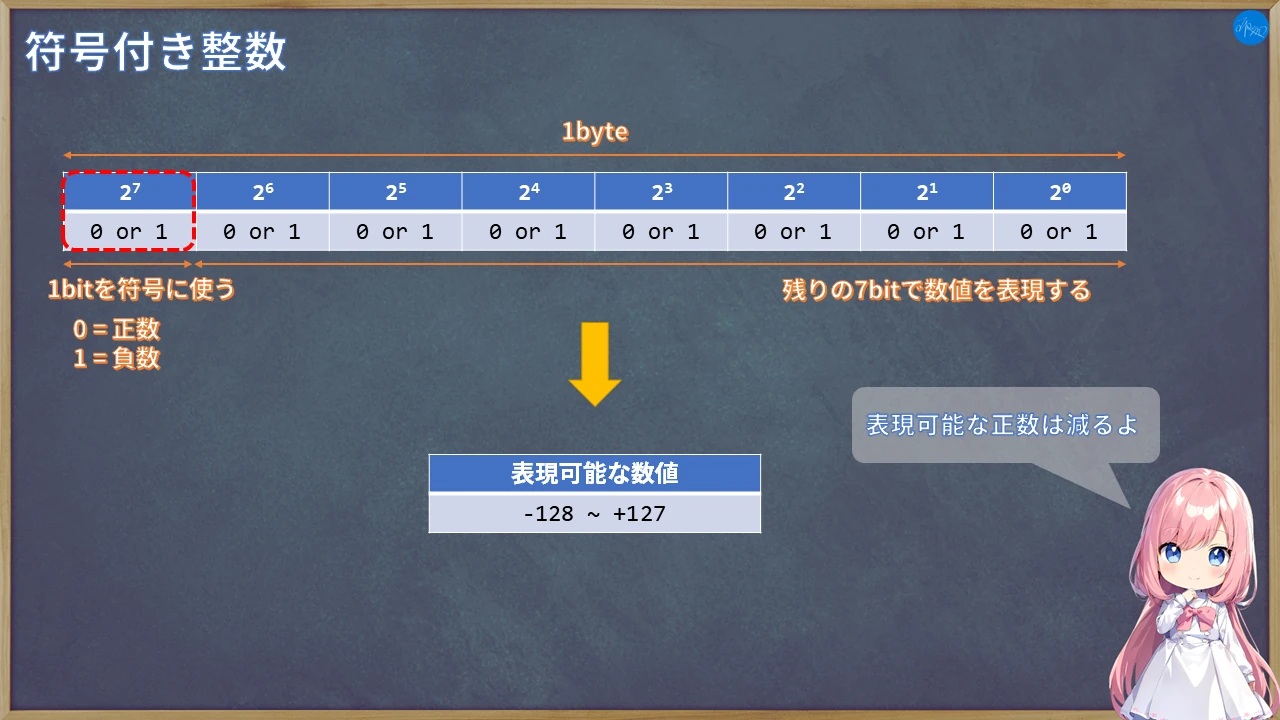
符号付き(signed)整数
符号付きの場合、最上位のbitを符号として利用することをルールとして定めます。
そうすると残りのbitで数値を表現するため、最大値は約半分くらいになります。
と説明しましたが、残念ながらこの方法はコンピュータでは使われません。
コンピュータでは2の補数と呼ばれる仕組みが採用されてます。
2の補数
シンプルに残りのbitで数値を表現すればいいと思いきや、コンピュータには致命的な問題があります。
何を隠そうコンピュータは足し算しかできません。つまり頑張って負数を表現しても計算ができないのです。

また冗談を。

本当だよ。万能そうなコンピュータだけど全部足し算で演算してるんだ。
長くなるので、足し算しかできない理由や足し算で四則演算する方法は省きます。
興味ある人は自分で調べてみましょう。では、本題の2の補数についてです。
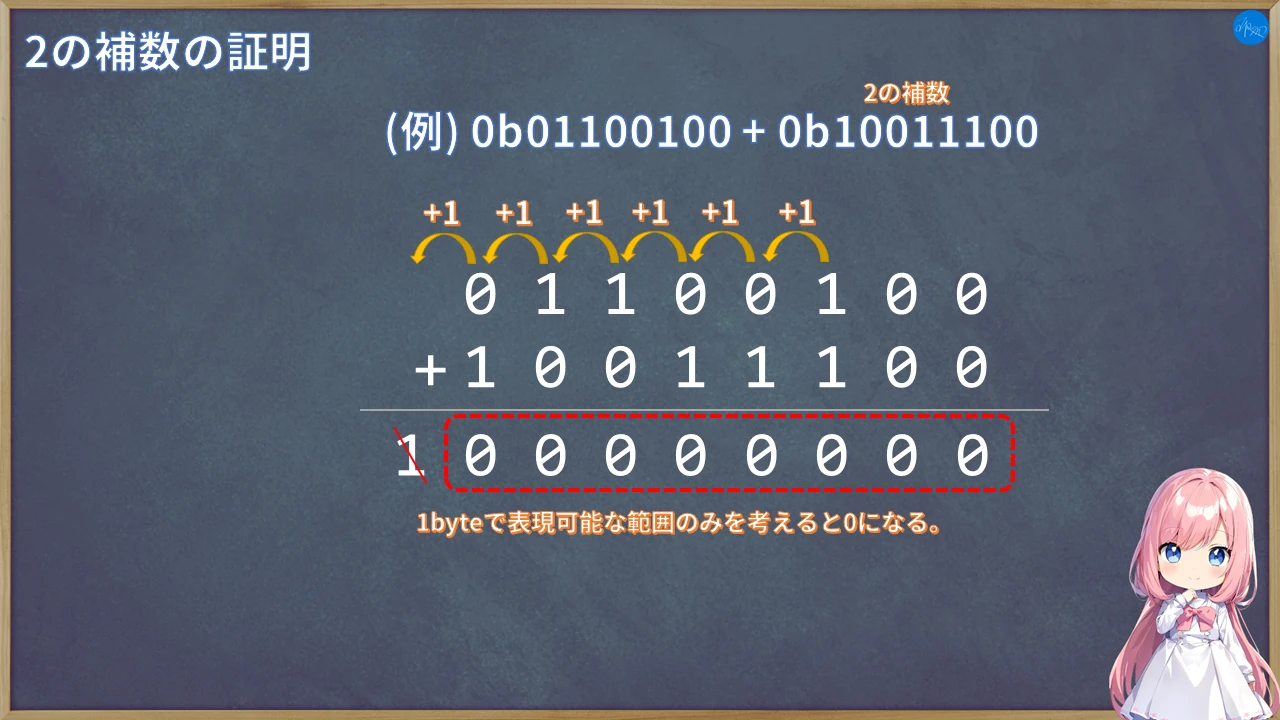
2の補数とは、ある数値の全てのbitを反転させて+1した数です。
と文字で書いても分かりづらいですよね。まず次の画像を見てください。

そして2の補数を利用すると言うのは、ある整数の2の補数で表現できる数値を負数にする考え方です。
つまり先程の例を使うと0b10011100の負数は0b01100100となります。
より意味不明になってきたと思いますが、この仕組みの何がいいのでしょうか。
これには先程の「コンピュータは足し算しかできない」が関係します。
先程の数字は10進数だと100になります。では-100とはどんな数字でしょうか。
それは両者を足すと0になる数字です。これを利用したのが2の補数です。

この仕組みを利用すると足し算で引き算が表現できるんだね。

考えた人は天才だよね。
小数点数の表現
小数点数の表現方法も2種類あります。
1つは小数点の位置が固定された固定小数点数、もう1つは固定されない浮動小数点数です。
固定小数点数
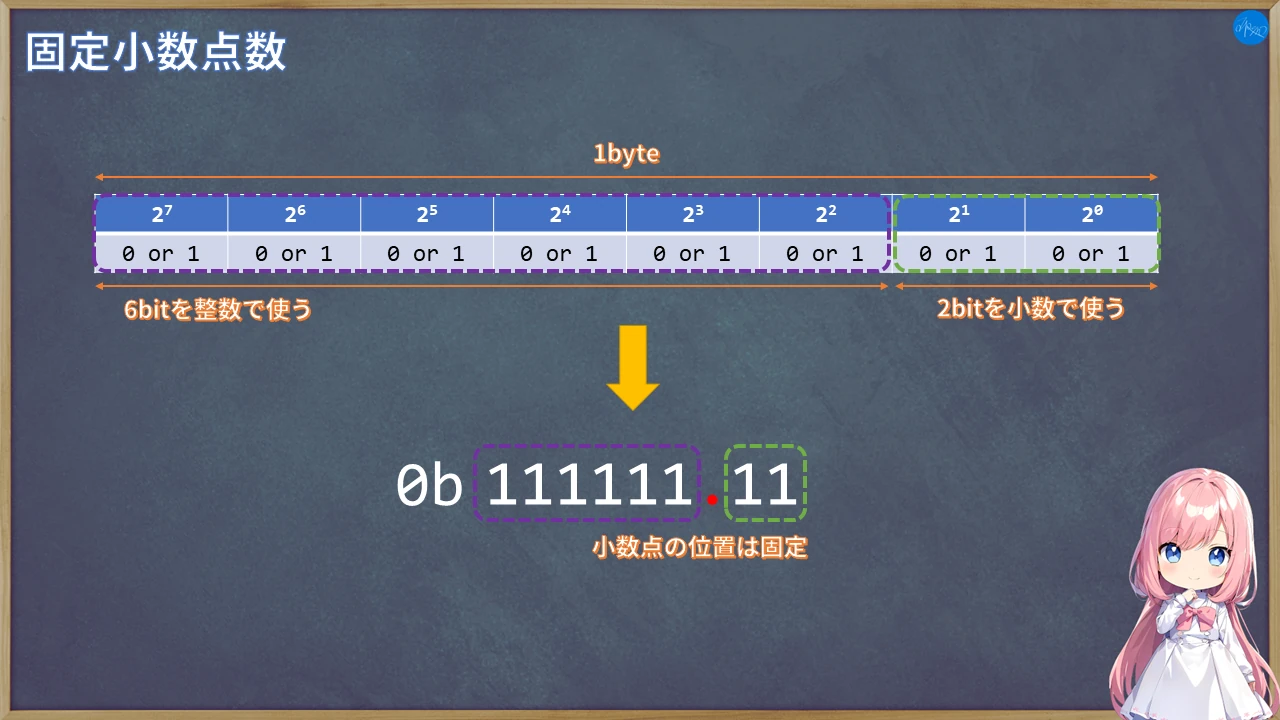
その名の通り小数点の位置が絶対値として固定され、常に同じ位置に存在します。
次の画像は上位6bitで整数部分、残りの下位2bitで小数点以下を表現するパターンです。
と言っても、実際に小数の表現に利用されるのは後に説明する浮動小数点数の方式です。
浮動小数点数
こちらは名前の通り小数点の位置が移動する方式です。
小数点の位置を固定すると無駄が発生するため、こちらの方式が利用されます。
各bitを符号部、指数部、仮数部と分けることで小数を表現します。
全体のbit数によって分割のルールは異なりますが、殆どの場合で32bitか64bitが使われます。

そもそも指数とか仮数って何?

その説明を用意したから見てみよう。


基数が10なのは10進数だからだよ。コンピュータが扱う場合の基数は2だね。

仮数とか指数が分かる形になってないと駄目なんですね。

うん。そしたら次は仮数や指数の割り振りだね。32bitのパターンを例に説明するね。
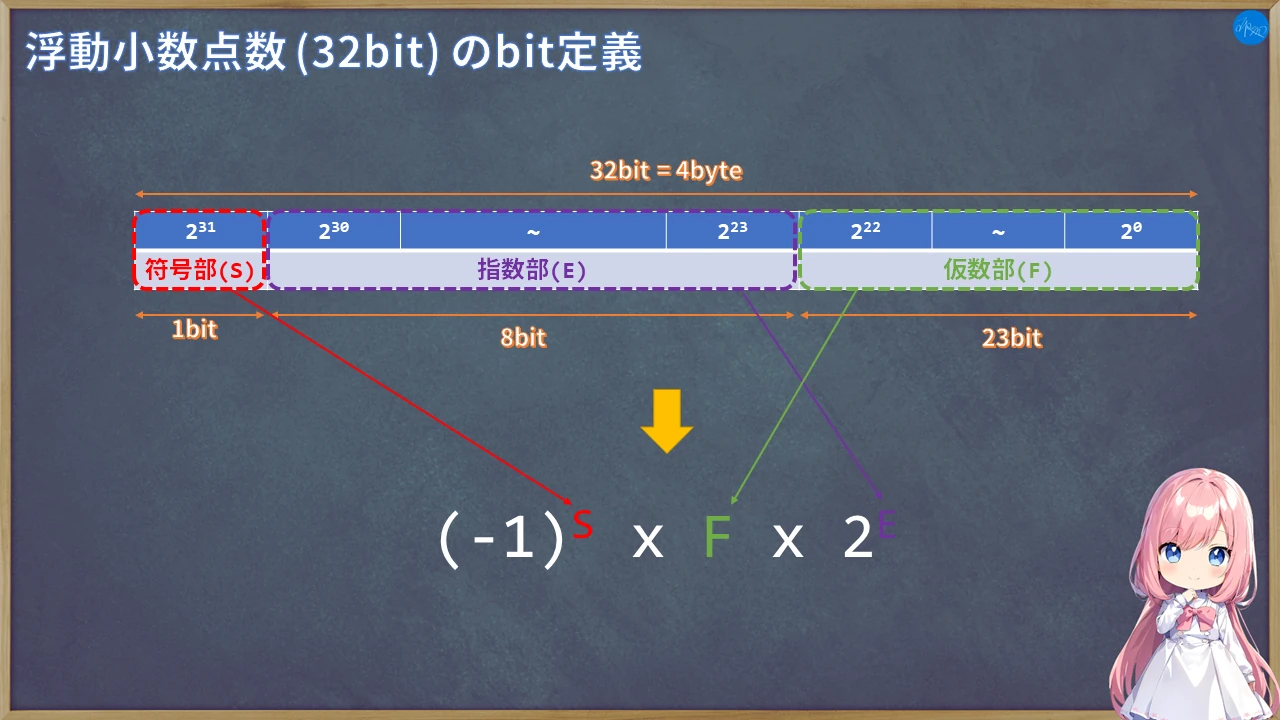

この図の通りに2進数にして配置すればいいの?

残念だけど、まだルールがあるよ。小数点の位置と指数に無限のパターンがあるのは10進数の説明で分かったよね。
当然2進数も同じなんだ。そんな自由な数字はbit化できないからルールを決めたよ。
この作業を正規化と言って、可能な限り多くの桁を表現するための仕組みでもあるよ。


この形式に合うように2進数を配置、それをbit化すれば浮動小数点数の完成だよ。


もう無理...

初心者が理解できたら凄いと思う。上にも書いたけど当時の自分は全く理解してないよ。

これを理解するメリットって何ですか?

それを聞かれると困る... ただ、確実に覚えて欲しいのはコンピュータは0と1でしか物事を考えないってこと。
正直、浮動小数点数の話は覚えなくても支障は無いと思う。実際のとこ僕も仕事に影響しなかったし。
あとがき
今は分からなくても再度戻ってくると簡単に理解できたりします。
挫折は勿体無いので、まずは先に進んでみてはどうでしょう。
◆ コンピュータサイエンスに関する学習コンテンツ
この記事は参考になりましたか?

コメント